By no means I am a good chess player. My chess.com rating oscillates around 1100 elo. But this game has something to it; even when I fail, I do enjoy playing chess.

It was a natural choice to try and write my chess engine. I went through some blog posts about techniques used to create strong chess engines, but at this stage of development, they weren't that useful.

What inspired me was a youtube video by Sebastian Lague: Coding Adventure: Chess AI. It gave me all the necessary pieces (pun intended) to start learning about how to create my own chess AI.

In this blog post, I'll go through some of the most interesting parts of this little chess engine I created.

But first, let's cover some basic stuff:

Tech stack

I wanted to build a web version of the engine. So the natural choice for me was to go with Typescript and React.

I chose a component library - Chakra UI, styled-components for some more advanced css and used Parcel to bundle my assets together.

And finally, I chose to host it on Netlify.

So far, so good.

User interface

To generate a chessboard in React I created a simple function that creates an array of 64 elements and calculates if the square should be white or black.

 const chessboard = Array(64)
  .fill('')
  .map((_, i) => {
    const squareColor =
      (i + Math.floor(i / 8)) % 2 === 0
        ? 'var(--light-square)'
        : 'var(--dark-square)'

    const file = 'abcdefgh'[i % 8]
    const row = -Math.floor(i / 8) + 8

    return { squareColor, file, row }
  })

I then modified this function to render a <Tile /> component, passing all the necessary props and rendering it using CSS-Grid.

After adding some more CSS the result was:

Nice.

The next step was to draw some pawns and pieces on the board.

I downloaded a chess pieces graphic from Wikipedia and created sprites for each pawn/piece like this:

const PieceIcon = styled.img.attrs({ src: pieces })<{
  piece: string
  color: string
}>`
  object-fit: none;
  object-position: 0 0;
  width: calc(60px * 8);
  height: calc(60px * 8);
  transform: scale(0.15);
  max-width: unset;

  @media (max-width: 1000px) {
    transform: scale(0.09);
  }

  ${calculateSpritePosition};
`

At this point I just wanted to write an AI for chess, so to handle game creation and chessboard management I used a josefjadrny/js-chess-engine library.

I use it to validate moves, generate a list of possible moves and for FEN parsing.

So, I loaded a FEN for starting chess position (rnbqkbnr/pppppppp/8/8/8/8/PPPPPPPP/RNBQKBNR w KQkq - 0 1)

After some FEN parsing and transformations, I could draw the pieces on the chessboard.

Yay.

Game state

To manage the state of the game I decided to use the Context API provided by React.

I created a reducer with the useReducer hook and connected it to the Context I created earlier.

This reducer is responsible for all the state changes in the game.

It also handles timers, turns and checks if the position is checkmate.

Developing the AI

When I had my front-end ready, it was time to start working on the engine itself.

I knew that the algorithm I needed to use was a recursive function, and therefore would block my event-loop until it finishes. This of course meant that my game would become unresponsive for a few seconds, each time a next move is calculated.

To workaround that I created a new function that spawns a Web Worker, runs the algorithm and returns a Promise, which is resolved once the move is found.

const runEngine = async (
  FEN: string,
  depth: number
): Promise<[string, string, number]> => {
  const worker = new Worker(new URL("./index.ts", import.meta.url), {
    type: "module",
  });

  const bestMove = await new Promise<[string, string, number]>((resolve) => {
    worker.addEventListener("message", (message: any) => {
      resolve(message.data);
    });

    worker.postMessage([FEN, depth]);
  });

  worker.terminate();

  return bestMove;
};

export default runEngine;

The logic behind this Web Worker is simple:

It receives a message containing details of the chess position (namely FEN), calculates the best move and sends it back.

import findBestMove from "./findBestMove";

addEventListener("message", async ({ data: [FEN, depth] }) => {
  const bestMove = findBestMove(FEN, depth);

  postMessage(bestMove);
});

The findBestMove function is just a wrapper for the more generic minimax function:

import minimax from "./minimax";

const findBestMove = (FEN: string, depth: number) => {
  const [evaluation, bestMove] = minimax(FEN, depth);

  return bestMove;
};

export default findBestMove;

How to find the best move

To understand how it can be done, we need to understand how chess positions are evaluated.

How can we decide who is winning?

We could simply calculate the points of the material for each player (a naive solution), then just subtract the points of the black player from the points of the white player.

So let's say that white has the advantage with 13 points and black has 10 points:

eval = 13 - 10 = 3

However, if black has the advantage, let's say 15 to 5, the evaluation would be:

eval = 5 - 15 = -10

This means that if white has the advantage the eval is a positive number, whereas if black has the advantage the eval is a negative number. (This will be important later)

As I said this is a naive solution, and it would not work very well. In chess, there are a lot of positional nuances, so just counting the material points is not enough.

I've used the concept of piece square tables. It states that, if a specific piece stands on the best tile for its type, it can get bonus points.

Let's use a rook square table as an example (from white's perspective):

const rookTable = [
  0,  0,  0,  0,  0,  0,  0,  0,
  5, 10, 10, 10, 10, 10, 10,  5,
 -5,  0,  0,  0,  0,  0,  0, -5,
 -5,  0,  0,  0,  0,  0,  0, -5,
 -5,  0,  0,  0,  0,  0,  0, -5,
 -5,  0,  0,  0,  0,  0,  0, -5,
 -5,  0,  0,  0,  0,  0,  0, -5,
  0,  0,  0,  5,  5,  0,  0,  0
]

As we see, we grant additional points for a rook if it's on the 7th rank. But we deduct points if the rooks stand either on the a or h file - because rooks are usually useless there.

That means that a well-positioned rook is worth more points of material than a poorly positioned rook.

Now we can sum the material points and add the bonuses for properly positioned pieces. This should be a good start for our engine.

But how can we calculate what is the correct sequence of moves to get to the best possible solution?

The minimax algorithm

The minimax algorithm is very useful for creating an AI for turn-based games. It minimizes the possible loss in the worst-case scenario and maximizes the gain in the best-case scenario, exactly what we want in chess. Our best move is worthless if the opponent's response will be even better for him. Because of that, we need to simulate the best possible moves for an engine, but also the opponent. That's a lot of work to do for a computer. So we will start small, with a depth of 3.

It means that we will try to predict 3 moves ahead, and then evaluate the position. If it's good for us, the engine will play it. If not, it will disregard it.

Here is the code:

import evaluate from "./evaluate";
import jsChess from "js-chess-engine";

const minimax = async (
  FEN: string,
  depth: number,
  alpha: number,
  beta: number
) => {
  if (depth === 0) return evaluate(FEN);

  const board = jsChess.status(FEN);
  const moves = jsChess.moves(FEN);
  const startingPoints = Object.keys(moves);

  const possibleMoves = startingPoints.reduce(
    (all: [string, string][], current: string) => {
      const movesFromThisPosition = moves[current].map((move: string) => [
        current,
        move,
      ]);

      return [...all, ...movesFromThisPosition];
    },
    []
  );

  if (board.turn === "white") {
    let maxEval = -Infinity;
    let newAlpha = alpha;

    for (const [from, to] of possibleMoves) {
      const newFEN = jsChess.move(FEN, from, to);
      const evaluation = await minimax(newFEN, depth - 1, newAlpha, beta);
      newAlpha = Math.max(alpha, evaluation);

      if (beta <= newAlpha) break;

      maxEval = Math.max(maxEval, evaluation);
    }

    return maxEval;
  } else {
    let minEval = Infinity;
    let newBeta = beta;

    for (const [from, to] of possibleMoves) {
      const newFEN = jsChess.move(FEN, from, to);
      const evaluation = await minimax(newFEN, depth - 1, alpha, newBeta);
      newBeta = Math.min(beta, evaluation);

      if (newBeta <= alpha) break;

      minEval = Math.min(minEval, evaluation);
    }

    return minEval;
  }
};

export default minimax;

That's a lot of code.

Let's explain what it does.

We run a minimax algorithm for each possible move, then if the depth has reached 0, we evaluate the position. However, if the depth is not 0, we get the new list of all possible moves in this position, and recursively run minimax again.

We store the best evaluation, and with each move, we compare if it's better than the previous iteration. Using this technique we can easily find the move sequence that will have the best result.

But there is one problem. It's slow. Like really slow.

That's because we are doing a lot of computations. Is there any method that could help us to speed things up?

Alpha-beta pruning

From Wikipedia, we learn that Alpha-beta pruning is a search algorithm that seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree.

I guess I won't be able to explain it better than Wikipedia, so here is an excerpt:

It stops evaluating a move when at least one possibility has been found that proves the move to be worse than a previously examined move. Such moves need not be evaluated further. When applied to a standard minimax tree, it returns the same move as minimax would, but prunes away branches that cannot possibly influence the final decision.

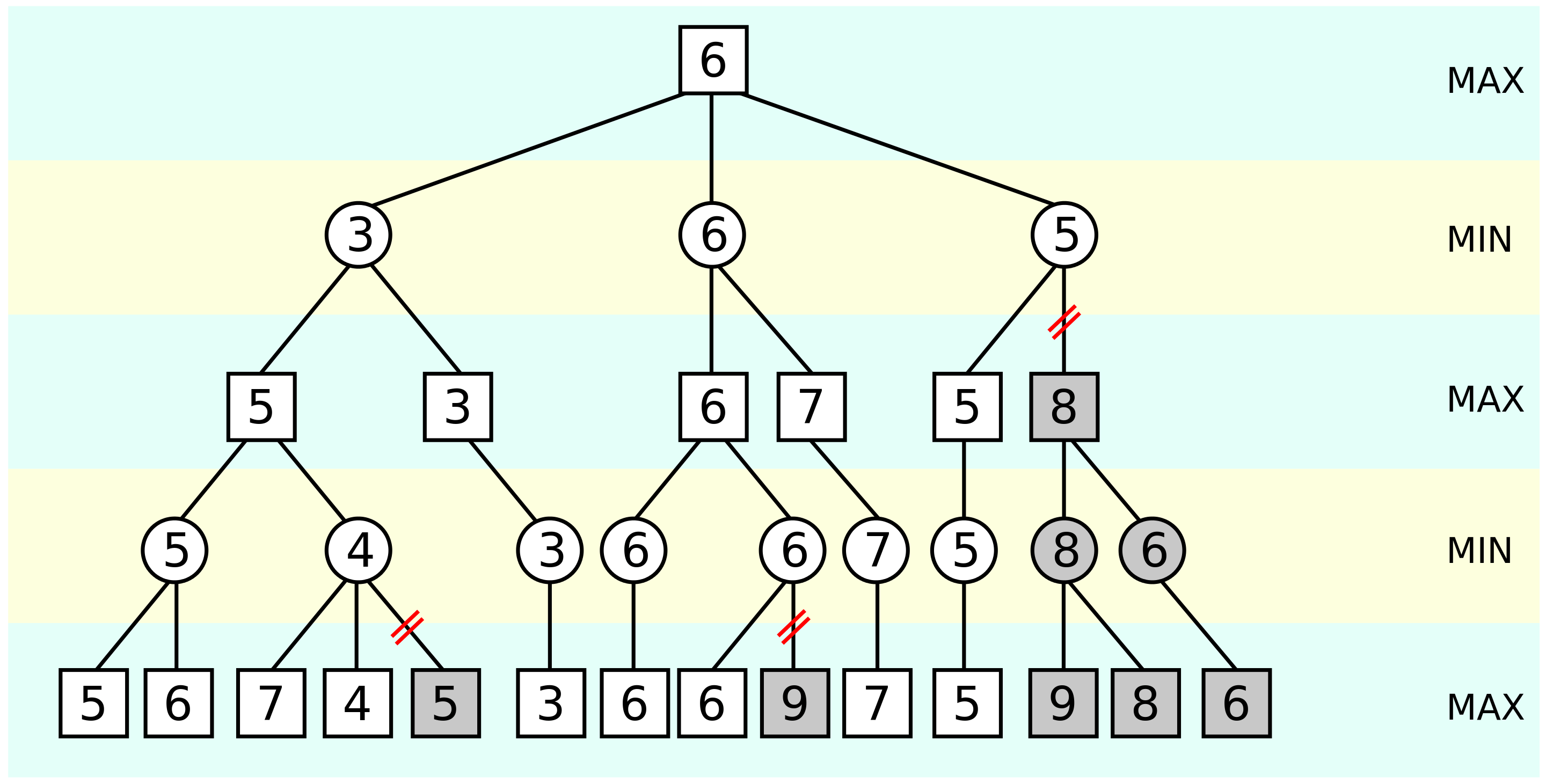
Ok, seems fine. It's a Win-Win situation. But how can we actually implement it?

We need to modify our minimax function.

The final version, after some refactoring, is:

const minimax = (FEN: string, depth: number): [number, Move] => {
  const board = jsChess.status(FEN);

  const alpha = -Infinity;
  const beta = Infinity;

  if (board.turn === "white") return maximize(FEN, depth, alpha, beta);
  else return minimize(FEN, depth, alpha, beta);
};

export default minimax;

We've extracted two functions minimize and maximize.

minimize function is responsible for finding the best move for black, and the maximize function does so for white. (Black has an advantage when eval is below 0, and white has an advantage when eval is above 0, remember?)

We also added two new variables that are passed down to these functions.

const alpha = -Infinity;
const beta = Infinity;

These variables will be used to calculate if we can prune the given branch.

Let's see how are they used in the maximize function.

const maximize = (
  FEN: string,
  depth: number,
  alpha: number,
  beta: number
): [number, Move] => {
  const game = jsChess.status(FEN);
  let move: Move = null;

  if (depth === 0 || game.isFinished) return [evaluate(FEN), move];

  const moves = getPossibleMoves(FEN);

  for (const [from, to] of moves) {
    const newFEN = jsChess.move(FEN, from, to);
    const [evaluation] = minimize(newFEN, depth - 1, alpha, beta);

    if (!move) move = [from, to];

    if (evaluation >= beta) {
      return [beta, [from, to]];
    }

    if (evaluation > alpha) {
      move = [from, to];
      alpha = evaluation;
    }
  }

  return [alpha, move];
};

This is a maximize function, so we are trying to find the best move for white. We are going through all possible moves and running the minimize function on the positions they create (simulating the next move done by black). If the evaluation is equal or greater than the given threshold (beta), we prune the tree, because further moves will not have any effect on the final outcome.

Something similar is done in the minimize function:

const minimize = (
  FEN: string,
  depth: number,
  alpha: number,
  beta: number
): [number, Move] => {
  const game = jsChess.status(FEN);
  let move: Move = null;
  if (depth === 0 || game.isFinished) return [evaluate(FEN), move];

  const moves = getPossibleMoves(FEN);

  for (const [from, to] of moves) {
    const newFEN = jsChess.move(FEN, from, to);
    const [evaluation] = maximize(newFEN, depth - 1, alpha, beta);

    if (!move) move = [from, to];

    if (evaluation <= alpha) return [alpha, [from, to]];

    if (evaluation < beta) {
      move = [from, to];
      beta = evaluation;
    }
  }

  return [beta, move];
};

Notice how the values of alpha and beta are changing: alpha is the evaluation of white's best move and beta is the evaluation of black's best move.

This can be used to decide which branches of the minimax tree can be pruned.

This is not a minimax nor alpha-beta pruning tutorial, so I'll wrap it up here.

The result

That's all that I needed to build a fully functioning offline chess game.

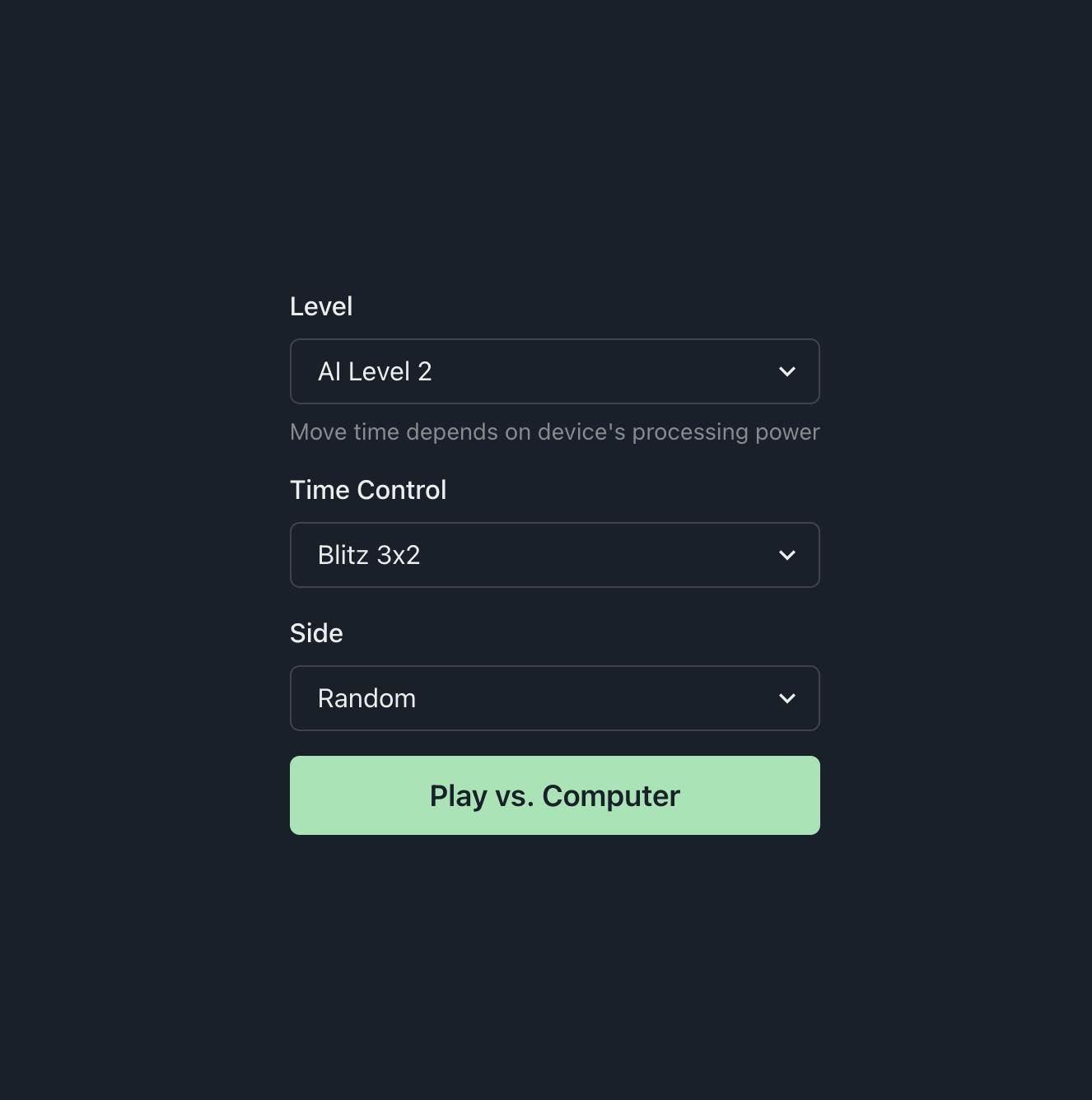
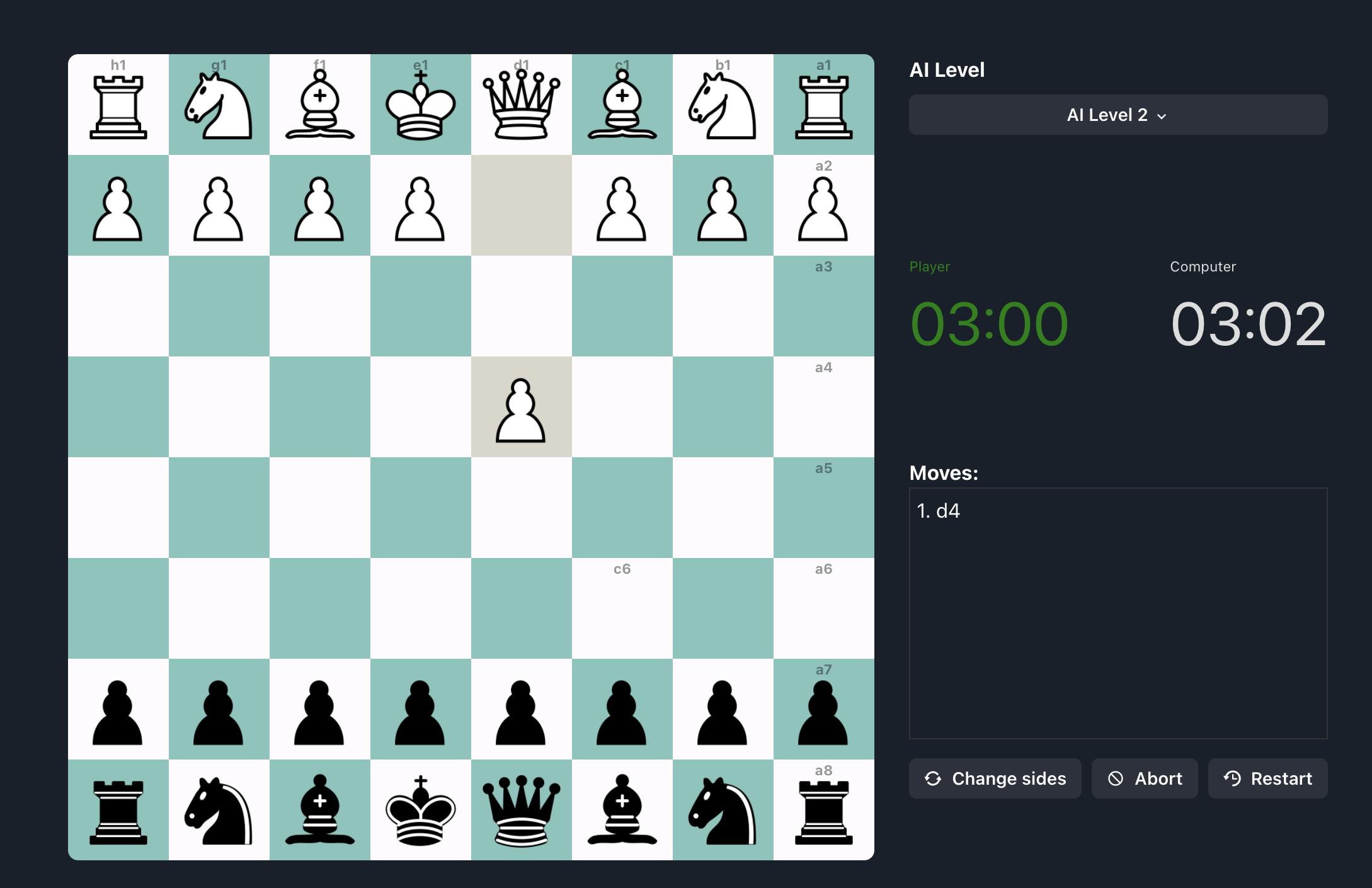
The final result looks like this:

Landing page:

Game view:

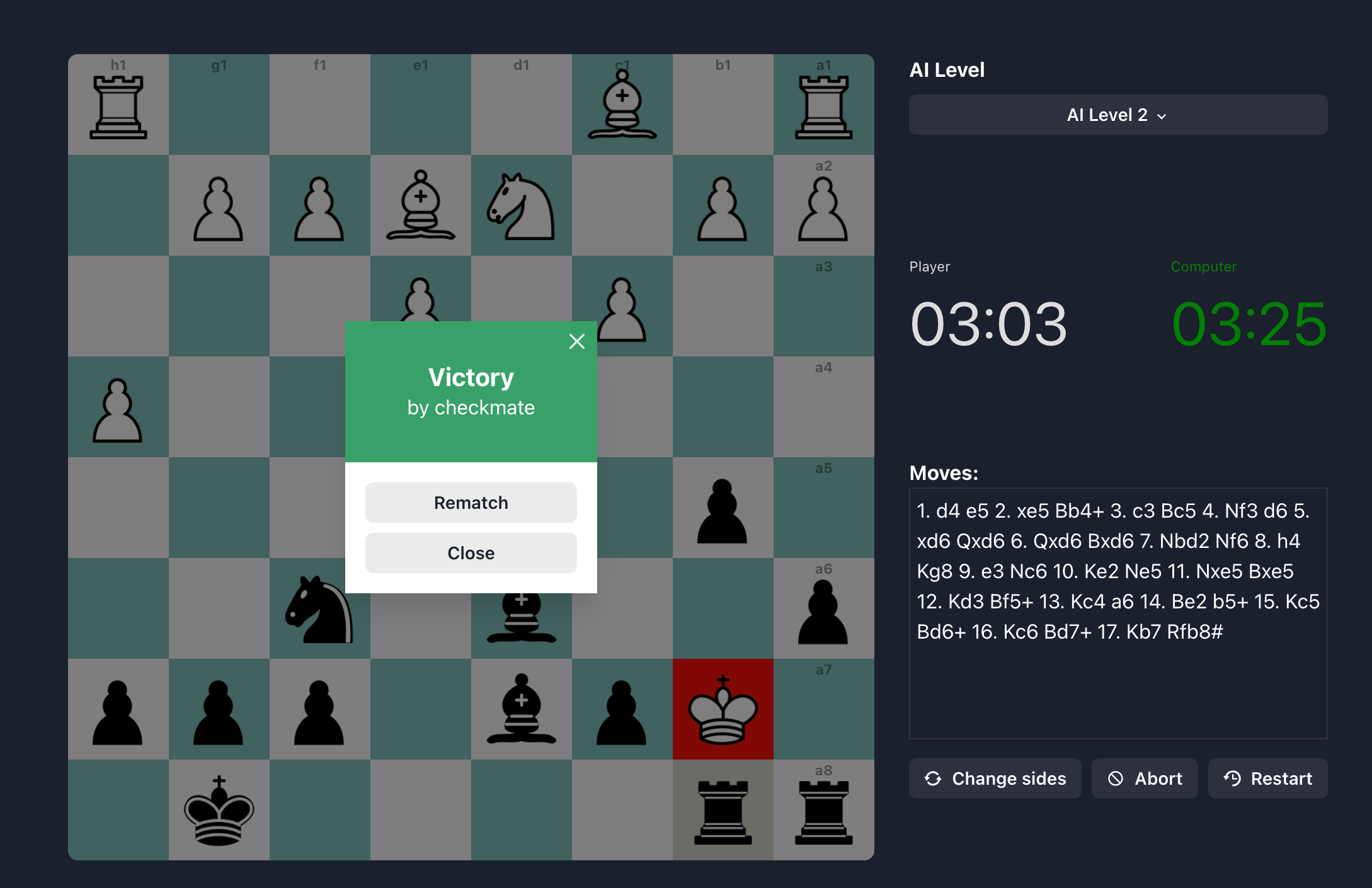
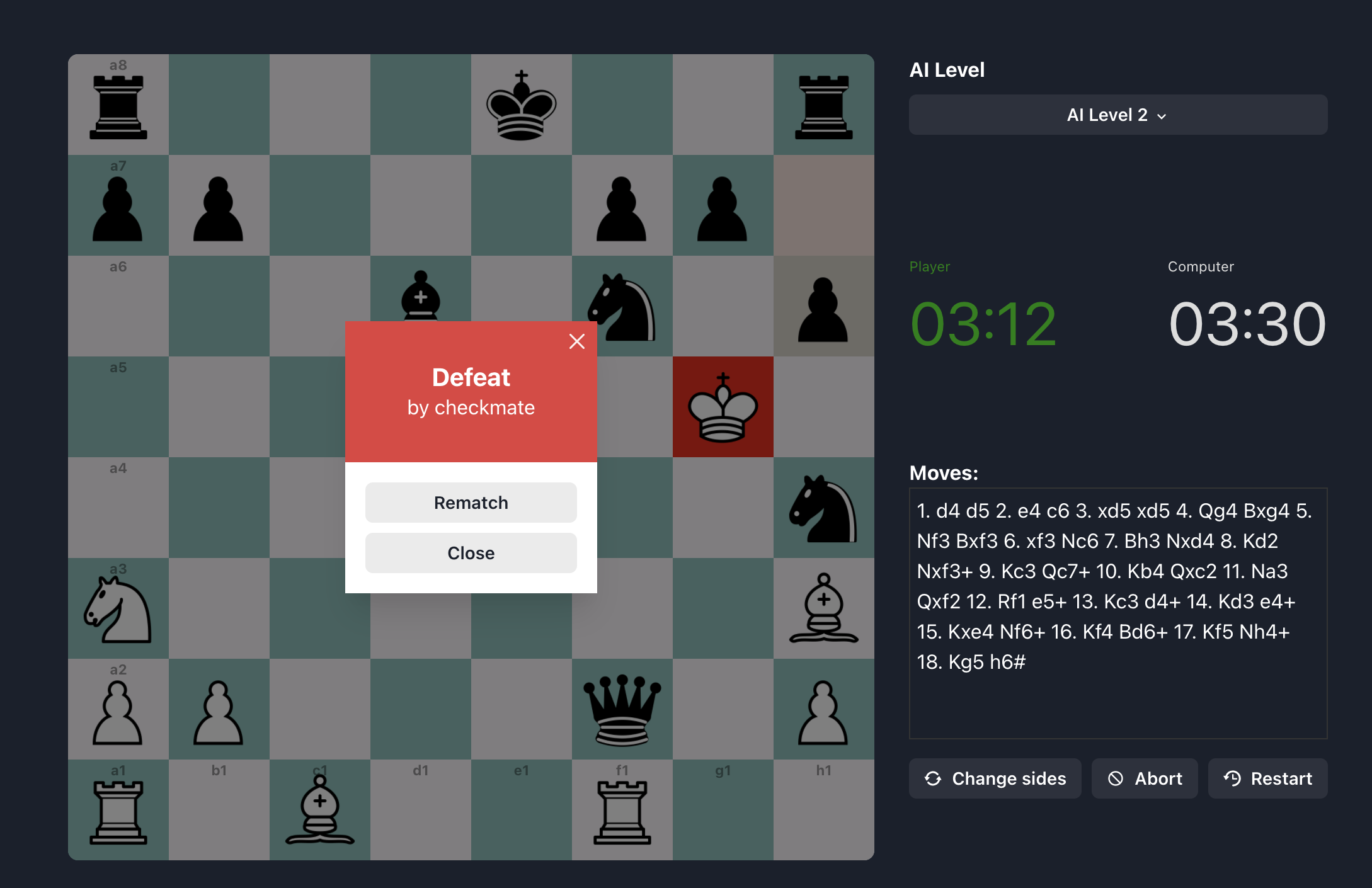
You can play this game here.

Please let me know what was the result :)

The complete code is hosted on my GitHub: